本稿では株式投資における「複利」が何を意味するのかを整理します。
「高配当株は複利効果が働くのでハイテク株やインデックスファンドより有利」
(ちょっと前にSNSで見た迷言)
「複利効果があるので資産運用は若い頃から始めるべき」
(インデックスファンドの神の神託)
こういった言説を批判的に検討する前提知識を提供したいと思っています。
個人的には、株式インデックスファンド等に過去の幾何平均収益率を適用し複利という言葉を使うのは誤解を生むのでやめた方が良いと思っています。自分も昔はマルキールやボーグルの本の影響で無批判に使っていましたが、5年ほど前からボラティリティを無視した右肩上がりの投資シミュレーションを見る機会が増えたので、この言葉はかえって有害だと考えるようになりました。
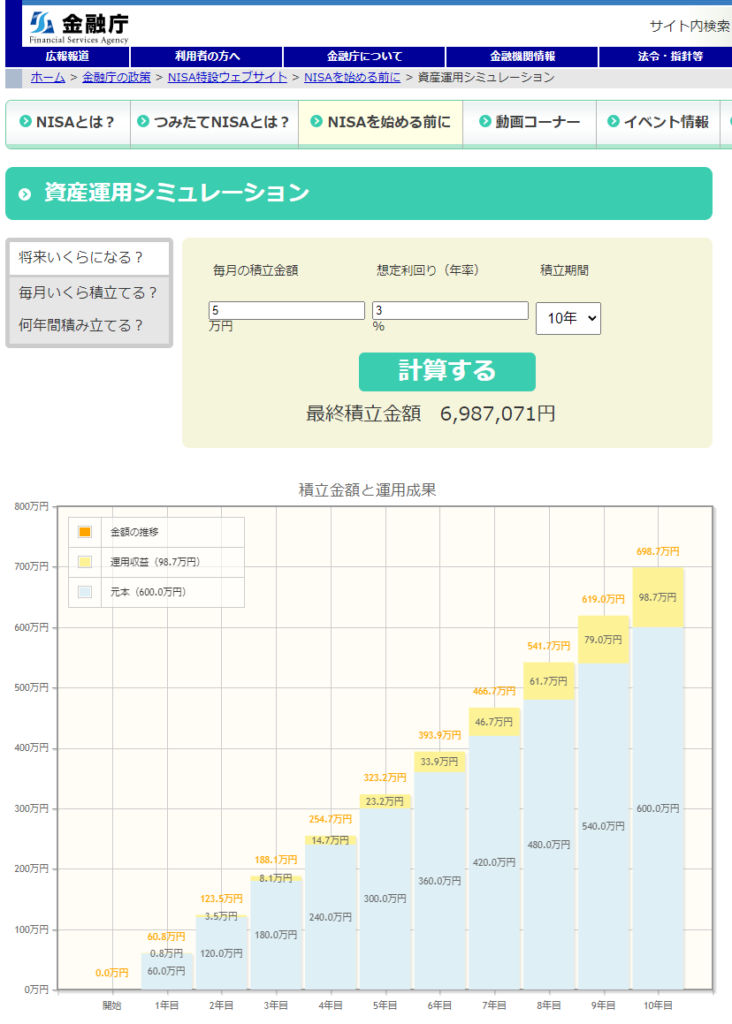
ボラティリティを無視した投資シミュレーションの例
出所:金融庁https://www.fsa.go.jp/policy/nisa2/moneyplan_sim/index.html
目次(クリックで各項目にジャンプ)
株式の複利?
ここもとの10年間で、ジョン・C・ボーグル(バンガード創業者)やバートン・マルキール(「ウォール街のランダム・ウォーカー」の著者)の影響から
「複利効果はすごい。資産運用は若いときから始めるべき!」
という言説を日本でもよく目にするようになった。
もともとは彼らの著書を読んだ勉強熱心な個人投資家による情報発信が多かったが、孫引き曾孫引きで理解が不十分な人も使うようになり混沌としてきているように思う。
株式は債券や預金ではない。
株式は上昇局面もあれば下落局面もある
株式の配当は利息と比べて不確定である
配当で株主還元する会社もあれば自社株買いを重視する会社もある
こういった特徴がある株式について「複利」という言葉を使うことに違和感がある人は少なくないと思う。
実際に、金融庁や金融機関も冒頭で述べたような単純な右肩上がりの積立シミュレーションを出しているが、彼らは慎重なのでこれに「複利」という言葉は使わない。
複利の基本と落とし穴
複利のポイント 商学部へようこそ
まず、本来的な複利の考え方を確認する。ファイナンスのテキストの最初に出てくるので内容的には商学部や経営学部の1年生レベル。
年利r%で年n回利払いの商品をT年間複利運用した場合の運用成果は以下の通り。
$$複利運用の成果=元本\times(1+\frac{r}{n})^{nT}$$
具体例を挙げると、10,000ドルを、税引き後年利3%、年12回利払いの米ドルMMFで3年間複利運用すると
$$10,000\times(1+\frac{0.03}{12})^{12×3}=10,940.51$$
となり、単利で運用した10,900ドルよりも40ドル多くなる。これが受取利息を再投資した分にも利息がついた効果、すなわち本来の複利効果である。
年間の利払い回数は金融資産・商品によって異なる。例示した外貨MMFでは1ヶ月分の分配金をまとめて支払うので年12回、普通預金は年2回利払い(厳密には利払いではなく「元加(がんか)」と呼ぶ)、日本国債は短期のものを除いて年2回利払いである。
この年間の利払い回数nを増やして行くと、早い段階で収束する。nが無限大のときを連続複利と呼び、
$$連続複利運用の成果=元本\times(e^{rT})$$
とネイピア数eで記述できる。計算が簡単になるので連続複利は学術研究ではよく使われているようだが、実務では具体的な商品ごとの利払い回数を使うことが多いと思う。
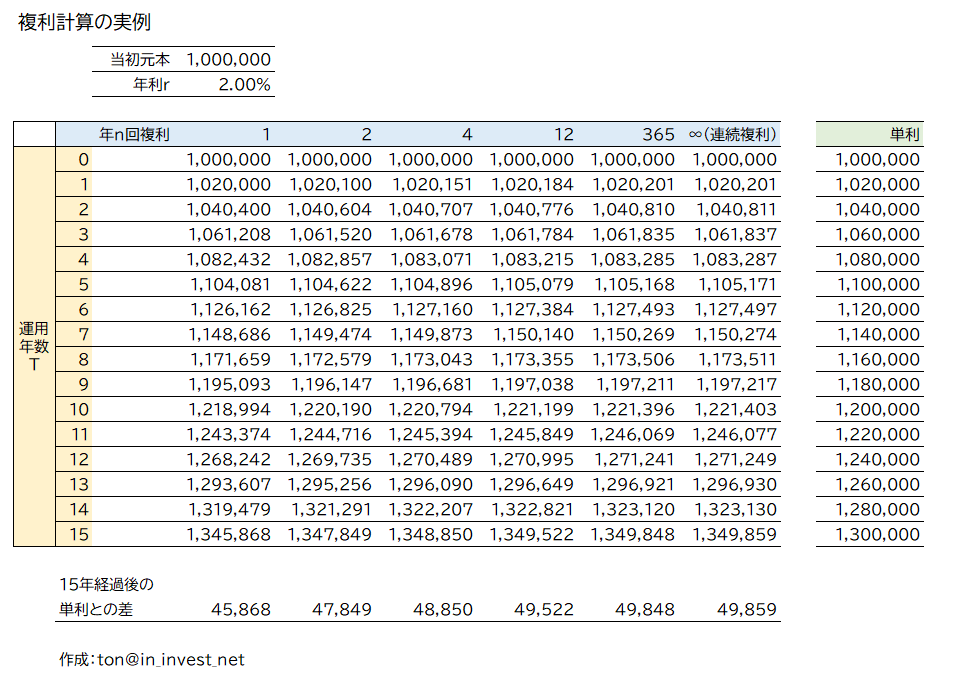
以下は、当初元本100万円を年利2%で運用する場合に、運用年数と複利回数でどの程度違いが出るのかを表にしたもの。単利と複利の差ははそれなりに大きいが、年間の複利回数による差は小さい。
再投資の利回りは債券でも預金でも「予想」
複利のリターンを考えるうえで、重要な割にあまり本には書いていないことがある。
それは、受取利息を再投資する時の利回りはその時になるまでわからないことだ。現在の利回りが2%の債券から半年ごとにいくらの利払いがあるかは分かるが、それを再投資する時の利回り水準は現時点では分からない。これが債券運用で重要になる再投資リスクである。
これまで見てきた複利計算では、元本に適用される単一の利回りrが受取利息の再投資にも適用されるものと単純化して計算されている。
※金利の日々の変動を観測できるようになったのは人類史ではつい最近だが、複利のアイデアはもっと古くからあったということなのかも。
株式は「複利」に馴染まない
このような本来の「複利」の考え方は、株式にそのまま適用するには無理がある。
第一に、元本確保の確実性が高い預金、MMF、国債の満期保有と異なり、株式のリターンは株式の価格変動(キャピタルゲイン)の影響を大きく受ける。
また、株式の配当は企業業績によって変動するため、単一の利回りrで投資期間全体と再投資分をカバーすることにも馴染まない。
従って「株式の複利」が嘘くさいと思う人は正しい。ちゃんと考えている証拠だと胸を張っていい。
株式の複利とインデックスファンドの神
本来の複利の計算はキャピタルゲイン、インカムゲインともに変動が大きい株式には馴染まないはずなのだが、対象が個別の株式ではなくインデックスファンドになると、指数の配当込みの年率幾何平均収益率を使って「複利計算」することがよく行われている。
幾何平均収益率とは(別の場所ではCAGRとも)
幾何平均収益率というのは、ある期間の収益率を累乗根で平均に引き直したものだ。例えば、ある資産の10年間の収益率が、
(1+1年目の収益率)×(1+2年目の収益率)×・・・×(1+10年目の収益率)=1.3439
だったとすると、元本分の1を引いた0.3439=34.39%がこの10年間の総収益率である。
ここで、
$$1.3439=(1+r)^{10}$$
となるrがこの資産の1年あたりの幾何平均収益率である。実際に計算するとrは3%になる。
※Excelなら1.3439^0.1で計算しよう。0.1乗が10乗根ということ。
現実の例として、2013年から2022年までのS&P500のグロス配当込みリターンで同様の計算をすると以下のようになる。
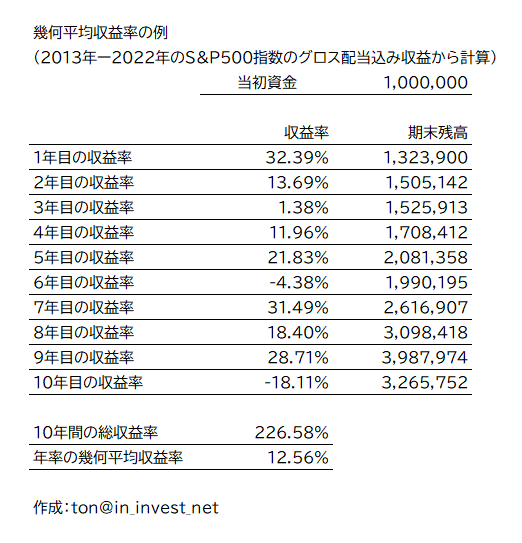
$$(1+2.2658)=(1+0.1256)^{10}$$
という関係である。
幾何平均は複数期間の変化率を平準化する正しい方法なので、収益率の計算以外でも使われる。特に売上高や市場規模の年率成長率として使われる場合はCAGR(Compound Annual Growth Rate, ケイガー)と呼ばれる。
幾何平均収益率によるインデックスファンドの複利計算
最初に見た複利計算を、インデックスファンド(≒株価指数)の年率幾何平均収益率をrにして書き直してみよう。rは年率の数字なので年間の複利回数nは1になる。
$$インデックスファンド複利運用の成果=元本\times(1+r)^{T}$$
このrにS&P500指数の直近30年の幾何平均リターンである8%を入れると米国株ブームでよく見るようになった右肩上がりのチャートになる。
また、rを選択式にして積立で資金投入するように調整すると、金融庁や証券会社のホームページにある積立NISAシミュレーションになる。
こまで来ると、どこが複「利」なのかわからなくなってこないだろうか。
rは指数の配当込み平均収益率なので、これは配当利回り(≒利率)と配当(≒利息)の再投資にとどまらず、未実現のキャピタルゲインが成長することも含んでいる。
おそらく、英語のCompound InterestとCompound Return(幾何平均(Geometric Average)による平均収益率)の両方を「複利」と訳したために複利の意味が広がってしまったのではないかと推測している。日英対照して確認したわけではないんだけど。
インデックスファンドの複利計算の問題点
このアプローチの問題点は収益率のボラティリティとドローダウンを無視していることだ。
株式リターンのボラティリティは高く、S&P500指数のような分散された株価指数であっても15%-20%程度になる。平均8%で標準偏差15%だとすると、マイナス側の1標準偏差は8-15=▲7%である。これは▲10%程度の下落に終わる年を日常的に想定すべき水準である。
また、大きな相場サイクルの中での最高値から最安値までの調整(ドローダウン)はマイナス50%に至る。S&P500のITバブル崩壊や金融危機時のドローダウンがおおむねこの程度だった。いずれも2000年以降の出来事である。
もちろん、長期平均のリターンには下落局面の損失が含まれている。S&P500の過去30年平均リターンの8%はコロナショックもリーマンショックもITバブル崩壊も含まれている。だが、平均の積み上げからは年度あたりの収益率のばらつきも、楽観と悲観を繰り返す相場サイクルのうねりも見えない。
インデックスファンドの神はどう使ったのか
現在私の手元にある資料で、指数の平均収益率による複利計算が書かれた最も古いものは、2000年に邦訳が出版されたジョン・ボーグルの著書「インデックス・ファンドの時代」である。
原著の"Common sense of Mutual Funds"の出版は1999年。翌2000年には、バンガード500インデックスファンドがフィデリティのマゼラン・ファンドを抜き米国最大の投資信託になった。記念碑的なタイミングで世に出た本だと言える。

本書でボーグルは以下の説明にこのアプローチを使っている。
①市場インデックスとアクティブファンドの平均の比較
執筆時の過去30年間の市場インデックスの平均収益率12.5%と同期間のアクティブファンドの平均収益率10.8%を比較し「この差は30年分にすると驚くべきことになる」と書いている。
②株式と安全資産の比較
年利5%の短期国債と平均収益率12%の株式を比較し、40年間運用すると極めて大きな差がつくと書いている。
③積立投資を早く始める利点
株式の平均収益率12%を前提に、50万ドルを貯めるために必要な積立額と年数を比較している。25歳から65歳までの40年間積み立てるなら月に43ドルで良い。だが、55歳からの10年で貯めようとするなら月に2,174ドルもの資金を用意する必要がある。冒頭でインデックスファンドの神の信託として挙げた「複利効果があるので資産運用は若い頃から始めるべき」はこれである。
もっとも、本書ではこの記述に至るまでに株式と債券のリスク/リターンの考え方を1章を使って解説しており、②と③の記述のすぐ近くにも「株式のリターンが確定利付的に機能するという印象をあたえるかもしれないが、決してそのようなことはない」「過去のリターンから将来のリターンを考える場合には注意が必要であり、リターンの推定は控えめにすべきである」と書かれている。
本書の時代では丁寧に使われていたこのアプローチが、時代の進展とともにが小さな注釈だけを伴って登場する様になったということなのかもしれない。
おわり:株式の複利の大本は企業収益の再投資
以上です。最後に「株式の複利」について自分の考えることを書きます。
株式の複利の大本は企業収益の再投資のことだと思う。
企業の当期純利益は、一部が配当として株主のもとに渡り、残りは利益剰余金(内部留保)として企業内で再投資される。そして、自己資本に対する利益率であるROEはこの再投資の収益性でもある。ROEが大切なのは自己資本の活用度合いというだけでなく、ゴーイングコンサーンで続いていく株式会社が、利益を企業内で再投資する時の収益率でもあるからだ。
株式の複利をこのように考えると、高配当株から得た配当を株主が再投資する場合も、グロース企業が配当せずに利益を内部留保として再投資する場合も複利効果はしっかりと機能している。違いがあるとすれば、高配当銘柄であれば配当金を再投資する投資家の銘柄選択能力が重要であり、企業内で再投資するグロース企業であればROEが重要なのだ。
もう一歩進めてこの考えをインデックスファンドに当てはめてみよう。
S&P500やMSCI ACWIに連動する分配なしの株式インデックスファンドを保有している場合は、2重の意味で再投資を行っていると言える。
1段階目→指数を構成する各企業は、配当に回さなかった利益を企業内で再投資している
2段階目→ファンドが保有銘柄から受領した配当金はファンド内で指数構成銘柄の株式に再投資されている
従って(当たり前だが)分配なしインデックスファンドをほったらかしにしている人も、株式の複利の恩恵を受けている。