ポートフォリオ理論の勉強をしていると、2証券ポートフォリオの分散(標準偏差)について手計算やExcelで計算する機会があります。
一方、3証券以上になると、教科書の説明もあまり深入りしていないものが多く、ウェブ上にも情報があまりありません。
理由は2つだと考えています。
①3証券以上のポートフォリオの分散は基本的に2証券の場合の考え方の拡張のため、理論としては特に面白くない
②計算式中の項数が証券数とともにどんどん増えるので、行列を導入する必要があるが、行列の演算がEXCELで出来ることがあまり知られていない。
(もちろんEXCELにこだわる必要はなく、プログラミング慣れしている人であればRやPythonの方が使いやすいかもしれません。)
本稿では、4資産(国内債券、国内株式、外国債券、外国株式)からなるポートフォリオについて、EXCELで分散を計算します。理屈の説明では「証券」、実際の計算では「資産」という言葉を使いますが、基本的に同じ意味で使っています。
私見ですが、個人投資家が教科書的なポートフォリオの最適化をしてみたいと考えた時に、一番ネックになる部分だと思います。是非参考にしてください。
目次(クリックで各項目にジャンプ)
分散共分散行列を用意する
分散共分散行列というのは、以下のように、資産(証券)の収益率の分散と共分散を行列としてまとめたものです。
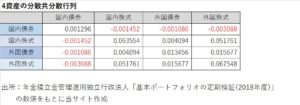
例えば、上の表だと、3行(外国債券)1列目(国内債券)の-0.001086は外国債券と国内債券の収益率の共分散です。また、2行(国内株式)2列目(国内株式)の0.063554は同じ項目なので国内株式の分散です(標準偏差(平方根)は0.25(25%)となり、実感に近いと思います。)。
自分で収益率の時系列データを用意できる場合はそこから計算しても良いですし、公的年金や運用会社が公表している相関係数行列から逆算しても良いでしょう。上のものも、出所のGPIFが年次資料で公表しているのは分散共分散行列ではなく、相関係数行列と各資産の標準偏差です。私が分散共分散行列の形に加工しました。
以下の方法で相関係数と標準偏差から簡単に共分散を得られます。
AとBの共分散=AとBの相関係数✕Aの標準偏差✕Bの標準偏差
※AとBが同じなら相関係数は1なので、標準偏差の二乗(=分散)になる
計算式に忠実に分散を計算する
ではポートフォリオの分散の一般的な計算式を見ておきましょう。
$$x_1からx_nまでのn証券からなるポートフォリオがあり、\\
それぞれの証券のウェイトをx_n、\\
それぞれの証券の収益率をr_nとすると、\\
ポートフォリオ全体の分散Var(r_x)は以下の通りです。$$
$$ Var(r_x)= \sum_{i=1}^N {x_i}^2Var(r_i)+2\sum_{i=1}^N \sum_{j=1+1}^N {x_ix_j}Cov(r_i,r_j) $$
式が面倒ですが、言っていることは単純です。
①全証券(資産)について、単一の証券のウェイトの二乗と分散を掛ける
②全証券の2種類ごとの組み合わせ(iとj)について、2、iのウェイト、jのウェイト、iとjの共分散を掛ける
③これまでの①と②で得られた項を全て足す
証券数をNとすると、①でN個、②ではN個から2つを選ぶ組合わせの数(C)だけ項が出てきます。4証券だと10項(4+6)です。4資産だけなのにかなり面倒です。
直感的に分かりやすい表にすると、以下のようになります。構成割合は適当な数字です。
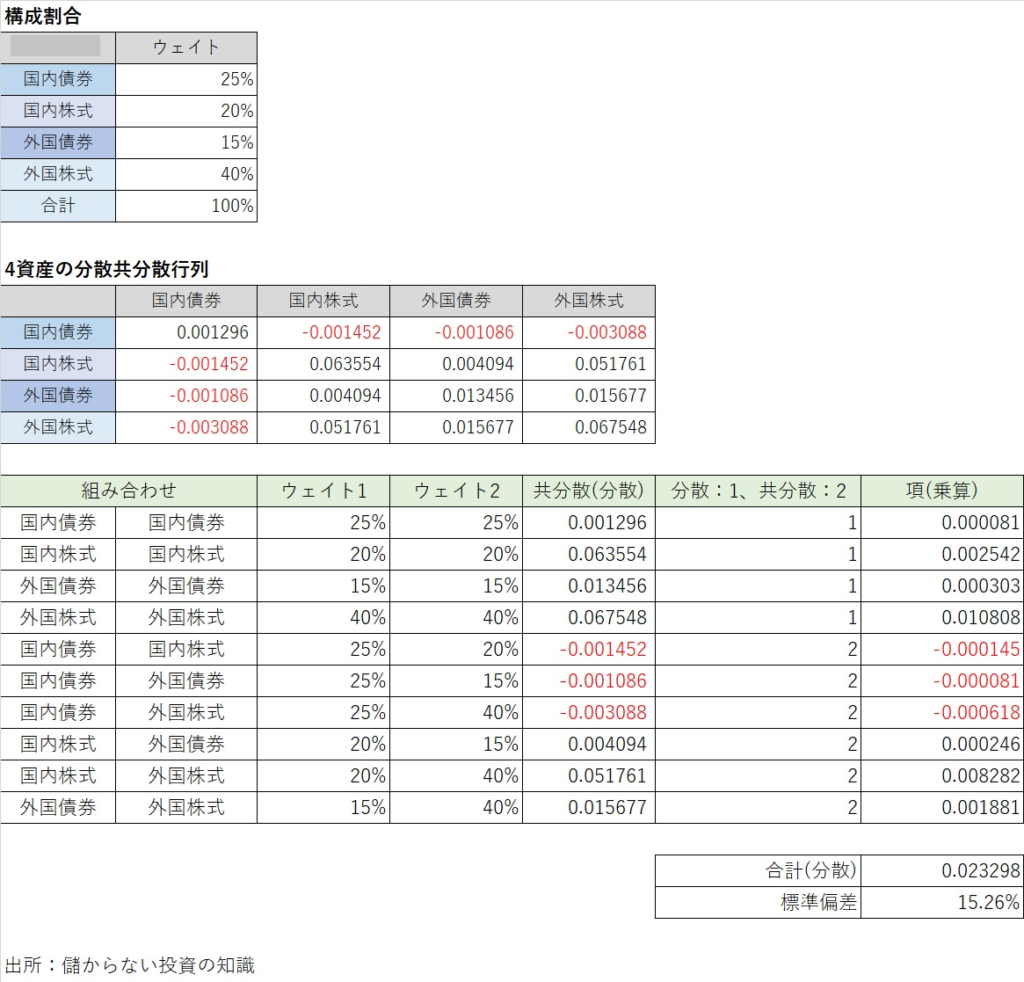
一番下の緑ヘッダーの表の各行が数式の個々の項に対応します。例えば、一番下の「外国債券」「外国株式」の組み合わせは、外国債券のウェイト15%、外国株式のウェイト40%、これらの共分散0.015677、共分散の項の係数の2を並べており、全てかけ合わせたのが「項(乗算)」の0.001881です。
各項の「項(乗算)」を足し合わせたものが「合計(分散)」です。つまり0.023298がこのポートフォリオの分散です。そして、平方根を取った15.26%がこのポートフォリオの標準偏差(ボラティリティ)です。内外株式65%のポートなのでこんなもんだと思います。
行列で計算する
数学的な詳細は省きます(私も完全には理解できていません)が、上記の分散の計算は行列式でも計算できます。結構高いですが、以下の本ではこの手のテクニックが豊富に紹介されています。
「ファイナンシャル・モデリング」サイモン・ベニンガ著 ロギカ書房
n種類の証券からなるポートフォリオで、各証券のウェイトをn行1列のベクトルとして並べたものをx、n行n列の分散共分散行列をS、xの転置行列をx^Tとすると、ポートフォリオの分散Var(rx)は以下のようになります。
$$Var(r_x)=x^TSx$$
これをExcelで計算する場合は以下のようになります
{=MMULT(MMULT(TRANSPOSE(xの範囲),Sの範囲),xの範囲)}
MMULTは行列式を計算する関数(MatrixMultipleでしょうか?)、TRANSPOSEは転置行列を返す関数です。
配列数式なのでセルへの入力を終えるときはCtrl+Shift+Enterを押します。
以下は、この方法で計算したものと、前項で計算したものを比較した表です。
一致していることが確認できると思います。
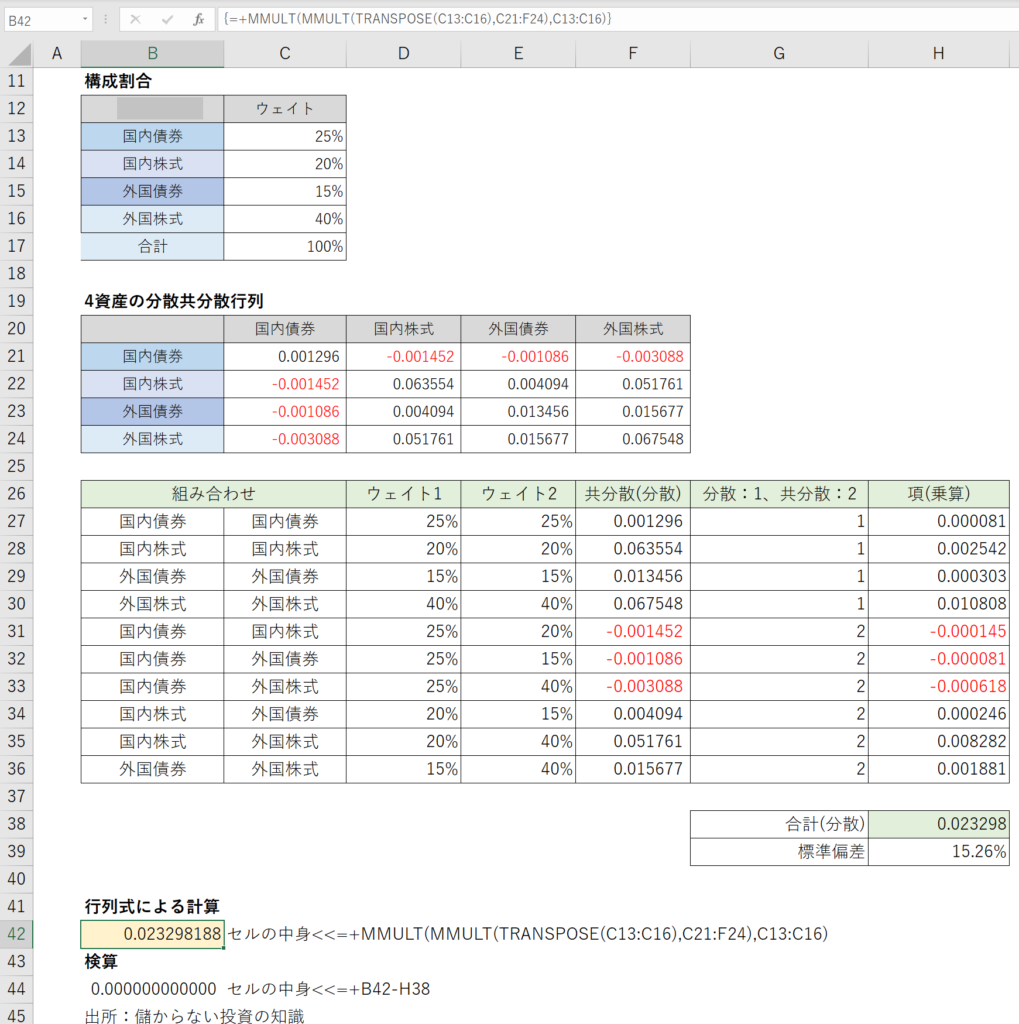
配列数式に抵抗がなければ、こちらの方が入力は簡単です。
おわり:資産配分の最適化の足がかりとして
本稿では、3証券以上のポートフォリオの分散の計算について解説しました。
これに加えて、ポートフォリオの期待収益率(ウェイトの加重平均で簡単に計算できます)があると、いろいろなことができるようになります。
シャープレシオの形にしたり、適当なリスク回避度を使って平均・分散効用の形にすれば、EXCELのソルバーで直感的に最適化計算ができます。
※シャープレシオ:シャープレシオ=(ポートフォリオの収益率ー無リスク資産の収益率)÷ポートフォリオの標準偏差。リスク水準を考慮した収益性の指標。
平均分散効用:U(効用)=ポートフォリオの収益率ーリスク回避度✕ポートフォリオの分散、となるような効用関数。
例えば以下の記事は、エクセルで株、債券、ゴールドからなる3資産で最小分散ポートフォリオやシャープレシオ最大化といった最適化を方法を解説したものですが、ポートフォリオの分散は本稿の方法で求めています。
-

Excelによるアセットアロケーションの最適化計算
本稿では、教科書的なアセットアロケーションの最適化計算をEXCELで行う際のアプローチについて解説します。 全世界株、米ドル建債券、ゴールド ...
続きを見る
Excelのソルバーは手軽なだけでなく、制約条件を勘案した計算が比較的簡単にできるのが利点だと思います。特に最適化の計算では、何も条件をつけないと、大きなショートポジションを含む極端な資産配分が出てくることがあります。このあたりはまた記事にしたいと考えています。
よろしければ参考にしてください。
