本稿では、教科書的なアセットアロケーションの最適化計算をEXCELで行う際のアプローチについて解説します。
全世界株、米ドル建債券、ゴールドの3資産のケースを例に、EXCELのソルバー機能を使って最小分散ポートフォリオとシャープレシオ最大化を計算します(効率的フロンティアは今回は無し)。
実際に手を動かして「最適化」と言っても快刀乱麻を断つようなソリューションではなく、インプットする数字や最適化指標の選択に大きく左右されるものだという実感を持っていただければ嬉しく思います。
目次(クリックで各項目にジャンプ)
関連記事
-

エクセルで3証券以上のポートフォリオの分散・標準偏差を計算する(分散共分散行列・MMULT関数)
ポートフォリオ理論の勉強をしていると、2証券ポートフォリオの分散(標準偏差)について手計算やExcelで計算する機会があります。 一方、3証 ...
続きを見る
教科書的な最適化計算のステップ
概要
ポートフォリオの最適化計算は、やること自体はシンプルです。
①最適化指標の決定
②指標を計算するための材料の収集
③何らかのエンジンで最適化処理を行い銘柄のウェイトを決定する
例えば、最適化指標をリスクモデルから得られる「推定トラッキングエラー」とし、推定トラッキングエラーが最小になるようにポートフォリオの最適化を行うと最適化法のパッシブファンド(インデックスファンド)になります。
投資対象銘柄や最適化する指標の計算に必要な項目が多くなると、専用の統計ソフトやポートフォリオ分析サービスが必要になります。
今回は、株・債券・コモディティ(金)の3種類のアセットクラスを対象に、期待リターン(収益率)とリスク(分散・共分散)のみに基づく最適化を行います。
この程度であればEXCELのソルバーで問題なく計算できます。
具体的には、以下の作業をします。
1.時系列データから分散・共分散行列を作成する
ポートフォリオのリスク(分散・標準偏差)を計算するために、各資産の分散と資産の組み合わせごとの共分散を計算します。
ここでは、代表的なETFの10年間の基準価額(NAV)から計算します。全世界株はACWI、米ドル建債券はAGG、ゴールドはIAUを使います。
iSharesは過去のファンドデータの開示が極めて充実しています。Vanguardのホームページは昔と比べると良くなっていますが、過去のNAVや分配金を確認するには不親切な設計です。
2.期待収益率を仮定する
リスクと違い、期待収益率は過去の実績値をそのまま使うのはNGという考えが一般的です。実績ベースの収益率は計算期間によって大きく変わるため実感とも整合的だと思います。
現在の時価総額から期待収益率を逆算するブラック=リッターマンモデルのようなアプローチが出てくるのはこのためです。
本稿では、過去10年平均と、ロボアドのWealthNavi社が資産運用サービスで使用している期待収益率を取り上げます。同社がブラック=リッターマンモデルで算出したものです。
3.指標を最適化する
最適化指標の選定は投資家の戦略次第です。
ここでは、まずポートフォリオの分散そのものを最適化指標とする最小分散ポートフォリオを計算し、続いて期待リターンと分散(標準偏差)からなるシャープレシオと平均・分散効用を取り上げます。
この計算は工学で二次計画問題と呼ばれるものです。
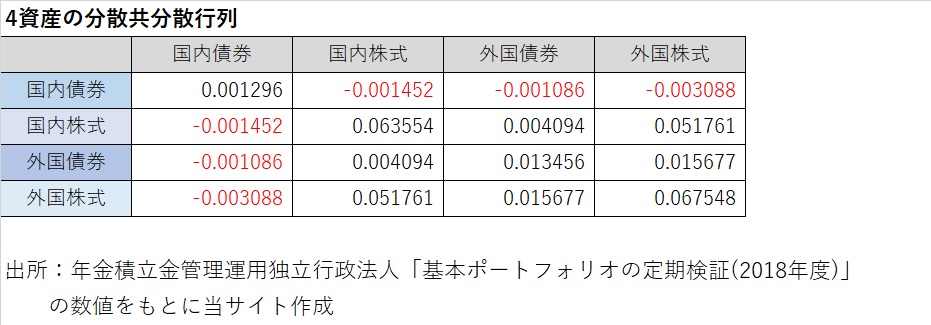
分散共分散行列とポートフォリオの分散
まず、分散・共分散行列を作成します。
2010年7月から2020年6月末までの10年間の、配当込み月次収益率で計算します。
過去に「Excelで3証券以上のポートフォリオの分散を計算する方法」という記事で詳しく書いているので、合わせてご参照ください。
-

エクセルで3証券以上のポートフォリオの分散・標準偏差を計算する(分散共分散行列・MMULT関数)
ポートフォリオ理論の勉強をしていると、2証券ポートフォリオの分散(標準偏差)について手計算やExcelで計算する機会があります。 一方、3証 ...
続きを見る
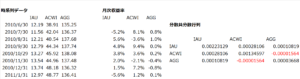
作業1 データの成型
iSharesの公式サイトから基準価額(NAV)のデータを取得します。
配当込み月次収益率となるように、以下の調整を行います。
①分配金を落ち日のタイミングでNAVに加算して分配金再投資ベースのNAVを計算する(iSharesのNAV情報はこの成型がとても簡単です)
②月次になるように月末の値をくくりだす
(「時系列データ」まで完成)
作業2 月次収益率の計算
収益率はシンプルに以下のように計算します(教科書では対数を使ってたりします)
7月のリターン=(7月末のNAV÷6月末のNAV)-1
(「月次収益率」まで完成)
作業3 分散共分散行列の計算
交差する資産の収益率の共分散になるように、分散共分散行列を作ります。
例えば、IAUとACWIが交差するところには
=COVARIANCE.S(IAUの月次収益率の列,ACWIの月次収益率の列)、
ACWIとACWIが交差するところには
=COVARIANCE.S(ACWIの月次収益率の列,ACWIの月次収益率の列)
という式が入っています。後者は同じ系列の共分散のため分散になります。
こだわりがなければCOVARUANCE.PよりCAVARIANCE.Sを使ったほうが良いと思います。
(分散共分散行列まで完成)
作業4 ポートフォリオの分散の形にする

最後にポートフォリオの分散の形にします。分散共分散行列(オレンジ色の部分)と、3行1列の資産ウェイトベクトル(青色の部分)から計算します。ウェイトは今は適当な数値で構いません。
基本に忠実な計算
分散=IAUのウェイトの二乗×IAUの分散+ACWIのウェイトの二乗×ACWIの分散+AGGのウェイトの二乗×AGGの分散+2×IAUのウェイト×ACWIのウェイト×IAUとACWIの共分散+2×IAUのウェイト×AGGのウェイト×IAUとAGGの共分散+2×AGGのウェイト×ACWIのウェイト×AGGとACWIの共分散
配列数式のよる計算
分散=MMULT(MMULT((TRANSPOSE(ウェイトベクトル),分散共分散行列),ウェイトベクトル)
(Ctrl+Shiftを押しながらEnter)
ここは特に以前の記事が参考になると思います。
分散共分散行列だけだとわかりにくいので、同じデータで計算した各資産の標準偏差を載せておきます。ゴールド>株>>債券の順にハイリスクです。
iShares ETFの10年間の実績リスク
| 資産 | ファンド | 月次標準偏差 | 年率換算 |
| 全世界株 | ACWI | 3.67% | 12.71% |
| ドル建債券 | AGG | 0.61% | 2.10% |
| 金 | IAU | 4.72% | 16.36% |
期待収益率の推定
次に、期待リターンを推定します。
冒頭で述べたとおり、とても悩ましい問題ですが、ここでは2つの収益率を見ます。
iShares ETFの10年間の実績リターン(2020年6月末基準)
| 資産 | ファンド | 10年実績リターン(年率) | 月次換算 |
| 全世界株 | ACWI | 9.31% | 0.78% |
| ドル建債券 | AGG | 3.73% | 0.31% |
| 金 | IAU | 3.31% | 0.27% |
出所:iSharesウェブサイト
WealthNaviが採用する期待リターン(2020年2月時点)
| 資産 | 同社区分 | 期待リターン(年率) | 月次換算 |
| 全世界株 | 米国株・日欧株・新興国株の単純平均 | 7.8% | 0.65% |
| ドル建債券 | 米国債券 | 2.3% | 0.19% |
| 金 | 金 | 3.8% | 0.32% |
どちらもそれほど大きくは変わりません。
他にも、GPIFや一部の運用会社がアセットクラス別の期待収益率を公表しています。
最適化計算
最後に、上で得た分散共分散行列と収益率から最適化目標を作成し、ソルバーで最適化します。
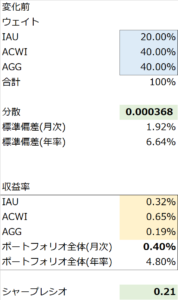
最適化指標の作成
最適化指標として、シャープレシオ(期待リターン÷標準偏差、リスク調整後収益率)と平均分散効用のセルを作成します。
シャープレシオのために、ポートフォリオの分散から標準偏差を計算します。「標準偏差(月次)」は「分散」の平方根(0.5乗)、「標準偏差(年率)」は「標準偏差(月次)」に√12(≒3.46)をかけて計算します。
また、WealthNaviの3資産の期待リターンをウェイトで加重平均し、ポートフォリオ全体の期待リターンを作ります。
ポートフォリオの期待収益率
=IAUのウェイト×IAUの期待リターン+ACWIのウェイト×ACWIの期待リターン+AGGのウェイト×AGGの期待リターン
ポートフォリオの期待収益率をポートフォリオの標準偏差で割ればシャープレシオの完成です。
もう1つの指標として、平均・分散効用を作ります(スクリーンショットから漏れていますがシャープレシオの下に作りました)。
これは投資家の効用を
効用(U)=期待収益率-0.5×リスク回避渡×ポートフォリオの分散
とするモデルです。
リスク回避度は投資家のリスク選好によって通常は1から10の間の値を取るとされています。
今回は、リスク回避度5で計算します。
ソルバーによる計算
最小分散ポートフォリオ
まず、最小分散ポートフォリオを算出します。データ⇛分析⇛ソルバーを起動し、
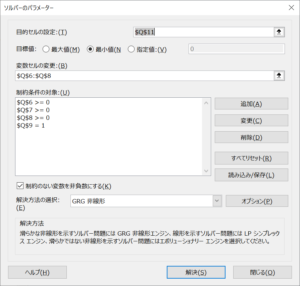
目的セルの設定にポートフォリオの分散のセルを指定、変更セルの変更にウェイトの3セルを指定します。最小分散ポートフォリオなので、目標値は「最小値」を選びます。
また、制約条件として、各資産のウェイトが0以上(ショート無し)とウェイトの合計が1(100%)になるようセルの条件を入れます。
これを「解決」すると、ウェイトが以下のように変わります。

最小分散ポートフォリオでは、ACWI3.7%、AGG96.3%になります。
この時のポートフォリオの標準偏差(年率)が2.04%です。債券(AGG)だけだと2.10%でしたが、債券よりハイリスクな株(ACWI)を加えるとポートフォリオ全体のリスクが下がります。これが分散効果です。
シャープレシオ最大化
同様に、シャープレシオを最大にするように最適化します。ソルバーの目標セルをシャープレシオに変更し、目標値は「最大値」を選びます。

ACWI9.10%、AGG90.90%でシャープレシオが最大になります。
リスクが高く、低相関とはいえ株と正の相関のゴールドは、シャープレシオの最適化の観点からは出番がないのかもしれません。
なお、ここで期待リターンをWealthNaviのものから実績10年平均に変えるとACWI7.18%、AGG92.82%でシャープレシオが最大になります。10年平均とWealthNaviで大きな差がなかったため、配分もあまり変わりません。
平均・分散効用の最大化
最後に、平均・分散効用を最大化するよう最適化したものが以下の結果です。
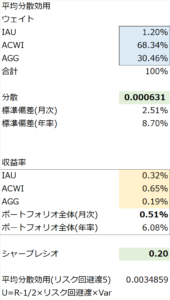
この結果では、シャープレシオよりも株の比重が高くなり、ゴールドも少し入ります。
おわり
以上です。
ポートフォリオの分散が分かっていれば最適化処理自体は簡単に出来たと思います。
一方で、実際に手を動かすと、最適化計算は、①インプット内容の差で計算結果が変わる、②インプットする数値の選定が難しい、③最適化目標の選定も難しい、といった困難を伴うことが分かります。
世に分散投資をウリにしたプロダクトは多くありますが、アセットアロケーションをあらかじめ固定(均等配分等)したものが多く、最適化を行う場合でも各資産のウェイトに上限・下限を設けます。
斜な見方ですが、実務者も教科書的な最適化をあまり信用していないのではないかと想像しています。